Para entender como realizar a multiplicação de frações nada melhor do que começar por identificar esta operação visualmente. Para isto vamos usar os exercícios do site "Visual fractions". Se você desejar recordar o método matemático para a multiplicação de frações clique aqui.
Para exercitar a multiplicação de frações vamos primeiro realizar a operação visualmente, através de figuras, isto é, vamos imaginar que estamos calculando a área de um retângulo. Os lados do retângulo são numerados como numa régua. Depois, e só depois, você deve fazer os cálculos matemáticos. Recomendamos que você faça os cálculos numa folha avulsa.
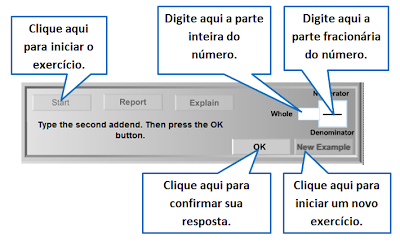
Clique aqui e abra a página dos exercícios. Clique no botão "Start". Você será apresentado a figura abaixo.
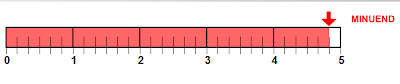
Aparecerá o primeiro fator, marcado em vermelho na horizontal. Leia na régua e digite a fração na forma mista no local indicado e clique no botão "OK". Se errar aparecerá uma mensagem de erro. O exercício avança somente quando você acertar. Tente novamente.
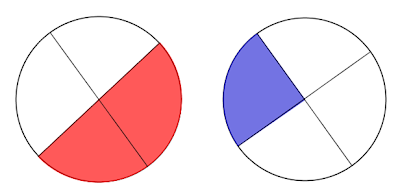
Quando acertar a fração aparecerá escrita em vermelho na parte inferior da página e o segundo fator será marcado, em azul, na vertical. Digite a fração no local indicado e clique no botão "OK". O processo se repete. Lembre-se: Se errar tente novamente.

Clique aqui e abra a página dos exercícios. Clique no botão "Start". Você será apresentado a figura abaixo.
Aparecerá o primeiro fator, marcado em vermelho na horizontal. Leia na régua e digite a fração na forma mista no local indicado e clique no botão "OK". Se errar aparecerá uma mensagem de erro. O exercício avança somente quando você acertar. Tente novamente.
Quando acertar a fração aparecerá escrita em vermelho na parte inferior da página e o segundo fator será marcado, em azul, na vertical. Digite a fração no local indicado e clique no botão "OK". O processo se repete. Lembre-se: Se errar tente novamente.

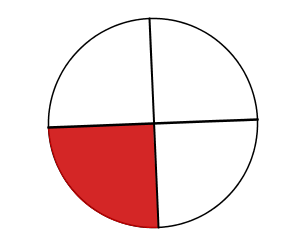
Quando acertar, a fração aparecerá escrita em azul na parte inferior da página. Escreva as frações na forma imprópria, numa folha avulsa, e faça os cálculos. Digite o resultado no local indicado.
Clique no botão "NEW example" para iniciar um novo exercício. Existem dezenas deles. Note que eles somente serão apresentados se você acertar o exercício anterior.
Clique aqui para iniciar os exercícios e bom estudo!

Clique na imagem e visite o site Visual Fractions, um guia visual para o aprendizado sobre frações.