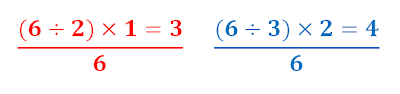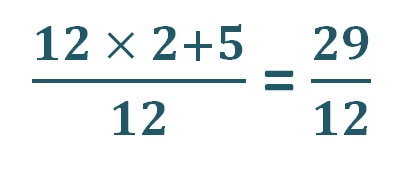Exercício - Adição de frações de mesmo denominador.

Para entender como realizar a adição de frações de mesmo denominador nada melhor do que começar por identificar esta operação visualmente. Para isto vamos usar os exercícios do site "Visual fractions". Se você desejar recordar o método matemático para adicionar frações de mesmo denominador  clique aqui.

Para exercitar a soma de frações vamos primeiro realizar a operação visualmente, através de figuras, isto é, vamos imaginar que estamos juntando pedaços de "pizzas" do mesmo tamanho. Depois, e só depois, você deve fazer os cálculos matemáticos. Recomendamos que você faça os cálculos  numa folha avulsa.

Para iniciar abra a página dos exercícios clicando aqui. Clique no botão "START" para iniciar o exercício. Será apresentada a figura abaixo:

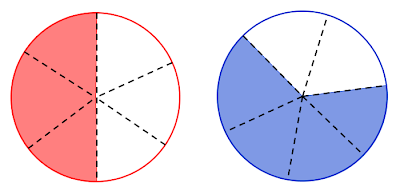
Observe as pizzas que aparecerão na tela. Os pedaços ainda não comidos estarão em vermelho. Digite, no local indicado na figura acima, o número que representa os pedaços não comidos das pizzas. Note que você deve digita-lo na forma mista, isto é, digite primeiro o número inteiro e depois a parte fracionária. Isto feito clique no botão "OK".

Se você digitou a resposta errada aparecerá a mensagem: "Incorrect. Please...". Tente novamente. Quando você acertar aparecerá a mensagem: "Type the second..." e a fração que você digitou será mostrada na parte inferior da página.

Observe a segunda série de pizzas que aparecerá na tela. Os pedaços ainda não comidos estarão em azul. Como da vez anterior, digite no local indicado o número que representa os pedaços não comidos das pizzas. Note que você deve digita-lo na forma mista, isto é, digite primeiro o número inteiro e depois a parte fracionária. Isto feito clique no botão "OK".

O processo se repete. Quando acertar aparecerá, na parte inferior da página, a segunda fração. Numa folha avulsa faça a soma das duas frações e digite o resultado como da vez anterior. Clique no botão "OK". Repita o processo até acertar. Quando isto acontecer o resultado correto da adição aparecerá na parte inferior da página. Veja a figura acima.

Analise o resultado e depois clique no botão "NEW EXAMPLE" para ter acesso a um novo exercício. Existem dezenas de exercícios distintos que são apresentados aleatoriamente à medida que você fornece a resposta correta do exercício anterior.

Para fazer o primeiro exercício clique aqui.



Clique na imagem e visite o site Visual Fractions, um guia visual para o aprendizado sobre frações.

Aula - Adição de fraçoes impróprias de mesmo denominador.

Grande parte das dificuldades apresentadas pelos  alunos do ensino médio no aprendizado de ciências e matemática não diz respeito aos conteúdos do nível médio mas às deficiências que eles trazem do ensino fundamental. Entre essas deficiências está a de não saber trabalhar com frações.

Se você tem essa dificuldade não adianta ficar se lamentando. Vamos trabalhar para elimina-la.

Nesta aula vamos trabalhar com a adição de frações impróprias de mesmo denominador. Se necessitar clique neste link e conheça o método para adição de frações de mesmo denominador. Para somar frações impróprias aplicamos o mesmo método com algumas particularidades que estudaremos a seguir.

Abaixo temos pizzas do mesmo tamanho. Algumas delas estão parcialmente comidas. Todas elas, as de cor azul e também as de cor vermelha, estão divididas em pedaços iguais.

Somar os pedaços que sobraram das pizzas azuis e vermelhas significa juntar os pedaços ainda não comidos como mostrado abaixo:

Ficamos então com três pizzas inteiras mais três quartos de uma outra pizza.

Em linguagem matemática, para somar os pedaços não comidos das pizzas azuis e vermelhas vamos, antes, representa-los  por frações impróprias. Na figura anterior as pizzas azuis e vermelhas são representadas pelas frações impróprias a seguir:

Se desejar clique aqui para rever o conceito de fração imprópria e como representar uma quantidade expressa na forma mista como uma fração imprópria.

Para somar as duas frações seguimos o método mostrado anteriormente neste link . Isto feito, ficamos com o seguinte resultado:

Se desejar você pode expressar o resultado na forma mista fazendo a divisão inteira do numerador pelo denominador da fração imprópria  e obter o resultado abaixo:

Imagem: portaldoprofessor.mec.gov.br

Aula - Adição de frações de mesmo denominador.

Grande parte das dificuldades apresentadas pelos  alunos do ensino médio no aprendizado de ciências e matemática não diz respeito aos conteúdos do nível médio mas às deficiências que eles trazem do ensino fundamental. Entre essas deficiências está a de não saber trabalhar com frações.

Se você tem essa dificuldade não adianta ficar se lamentando. Vamos trabalhar para elimina-la.

Nesta aula vamos tratar da adição de frações de mesmo denominador. Temos, na figura abaixo, duas pizzas de mesmo tamanho  divididas em quatro pedaços iguais. Os pedaços vermelhos e azuis são aqueles ainda não comidos.

Somar os pedaços de pizza que sobraram significa juntar os pedaços que ainda não foram comidos. Isto  está representado pela terceira pizza, na figura acima.

Em termos matemáticos esta operação de juntar os pedaços não comidos das duas pizzas é representada pela adição de duas frações como mostrado abaixo:

 

 Como você certamente já percebeu, quando somamos duas ou mais frações de mesmo denominador, obtemos uma fração com o mesmo denominador e cujo numerador é a soma dos numeradores das frações somadas.

Este processo vale tanto para frações próprias como para frações impróprias de mesmo denominador. Se necessitar acesse este link e recorde o conceito de fração imprópria.

Imagem: portaldoprofessor.mec.gov.br

Exemplo - Trajetórias.

No estudo do movimento dos objetos no espaço usamos alguns conceitos básicos. Entre eles está o de trajetória.

A trajetória do movimento de um objeto é o caminho percorrido por ele, isto é, o conjunto de pontos no espaço ocupados sucessivamente pelo objeto ao se movimentar de um ponto a outro do espaço. A forma desse caminho depende do observador.

Repare nas fotos a seguir. Elas fazem parte o álbum  AIRPORT   postado no flickr. Nessa série de fotos o fotógrafo americano Terence Chang usou a técnica de longa exposição para registrar as luzes de navegação e sinalização dos aviões em processo de decolagem ou aterrisagem.

O registro foi feito no aeroporto internacional de São Francisco, na California, durante o mês de julho de 2009. A longa exposição permite a materialização na foto da trajetória seguida pelos aviões através das suas luzes de navegação. Note que, ao contrário do que seria de se esperar, quando os aviões estão decolando ou aterrisando, as trajetórias seguidas por eles não são tão suaves. Existem mudanças bruscas de direção devidas aos ajustes realizados pelos pilotos.

Para ver a série completa acesse o álbum AIRPORT no flickr

Para conhecer o trabalho do Sr Terence Chang acesse a galeria exxonvaldez.

Informação via: Flowdata.com.

Exemplo - As camadas atmosféricas.

 O site "Our amazing planet" preparou um interessante cartaz onde mostra, em escala, as várias camadas que compõem a nossa atmosfera. Temos uma faixa de 350 km desde a superfície até a fronteira com o espaço. Embora, na escala humana, a atmosfera seja gigantesca, em comparação com nosso planeta ela não passa de uma fina camada de ar. Veja a figura abaixo:

Nossa atmosfera é divida em camadas de acordo com a densidade do ar, da temperatura, etc. O infográfico percorre todas estas camadas e mostra, em cada uma delas, os principais eventos e características. Mostra também a altitude da órbita das principais naves já lançadas.

Nossa jornada começa na órbita da Estação Espacial Internacional, na borda do espaço, a 350 km de altitude, passando pela altitude da órbita percorrida por  Yuri Gagarin em 1961 e indo até os 32 km de altura do salto em queda livre de Joseph Kittinger, em 1960.

As camadas de nossa atmosfera são:

• Troposfera - A camada mais próxima a superfície. Tem uma altitude que varia de 20 km no equador a 10 km nos polos. Contém a maior parte dos gases e quase toda a água. É nela que ocorrem todos os fenômenos que determinam o nosso clima. No topo a temperatura cai para -50 ºC e a pressão para 0,1 atm.
• Estratosfera - A primeira camada intermediária. Vai de 20 km a 50 km. Nela a temperatura aumenta até -15ºC e a pressão cai para 0,001 atm, no topo. Nesta camada o Oxigênio reage com a radiação solar e forma a camada de Ozônio que absorve a radiação ultravioleta do sol.
• Mesosfera -  A segunda camada intermediária vai de 50 km a 85 km de altitude. A Temperatura torna a cair  até -120 °C e também a pressão que chega a 0,0001 atm no topo.
• Termosfera -  A camada exterior da atmosfera vai de 100 km a 350 km. Nela existe grande interação entre as poucas moléculas de ar e a radiação solar. A temperatura chega a 2000°C. O ar ionizado reflete as ondas de rádio.

[Source: Telescopes for Beginners for OurAmazingPlanet.com]

Exercício - Compare duas frações.

Para entender como duas frações são comparadas nada melhor do que começar por identifica-las visualmente. Para isto vamos usar os exercícios do site "Visual fractions". Se você desejar recordar o método matemático para comparar duas frações clique aqui.

Neste exercício vamos treinar o que aprendemos sobre comparação de duas frações. A cada exercício serão apresentadas a você duas frações. Você terá que optar por uma entre três alternativas: As duas frações são iguais? A fração da esquerda é maior que a da direita? É menor?

Após clicar no botão "Start" você verá duas frações como na imagem abaixo:

O exercício consiste em responder a seguinte questão: A fração em vermelho representa uma quantidade maior, menor ou igual à fração em azul?

Para dar a reposta clique num dos botões "<", ">" ou "=" como indicado na figura abaixo:

Para ter acesso aos exercícios abra a animação. Faça os cálculos numa folha à parte. Um novo teste será dado somente depois que você responder corretamente o anterior.

Se você optar por clicar no botão "=" e esta for a resposta errada, verá a mensagem abaixo: A primeira fração não é igual à segunda fração.

 

Se você optar por clicar no botão "<" e esta for a resposta errada, verá a mensagem abaixo: A primeira fração não é menor que  a segunda fração.

Se você optar por clicar no botão ">" e esta for a resposta errada, verá a mensagem abaixo: A primeira fração não é maior que segunda fração.

Se você der a resposta certa o botão "New example" aparecerá em vermelho e o programa mostrará a figura:

Quando  reduziu as duas frações ao mesmo denominador você, na verdade, redividiu as duas pizzas na mesma quantidade de pedaços (ver linha tracejada). Com isto ficou fácil de comparar as duas frações. Veja a imagem acima. As pizzas foram divididas em 14 pedaços (linha tracejada). A fração não comida da pizza vermelha é maior pois tem 8 pedaços enquanto  a fração da pizza azul tem 7 pedaços.

Para começar abra a animação.   Bom estudo!





Clique na imagem e visite o site Visual Fractions, um guia visual para o aprendizado sobre frações.

Aula - Comparando frações.

Grande parte das dificuldades apresentadas pelos  alunos do ensino médio no aprendizado de ciências e matemática não diz respeito aos conteúdos do nível médio mas às deficiências que trazem do ensino fundamental. Entre essas deficiências está a de não saber trabalhar com frações.

Se você tem essa dificuldade não adianta ficar se lamentando. Vamos trabalhar para elimina-la.

Nesta aula vamos comparar duas frações, ou seja, vamos tentar responder as perguntas: Elas são iguais, isto é, elas descrevem quantidades iguais de uma grandeza? Uma delas é maior que a outra? é menor?

Se desejar recorde a definição de fração  clicando aqui.

Observe as duas pizzas abaixo. Os pedaços coloridos em azul e vermelho são aqueles que ainda não foram comidos. Repare que as duas pizzas foram divididas da mesma forma, ou seja, em oito pedaços iguais. Isto significa que, em termos matemáticos, as frações que representam os pedaços não comidos  das duas pizzas têm o mesmo denominador.

Decididamente elas não são iguais pois numa restam dois pedaços e na outra três pedaços. Saber qual delas é a maior também é fácil: Basta olhar! A fração que representa os pedaços não comidos da pizza azul é menor que a fração que representa os três pedaços não comidos da  pizza vermelha.

Comparar duas frações de mesmo denominador é fácil: Elas serão iguais se tiverem o mesmo numerador. A maior delas será aquela de maior numerador. Esta propriedade também sugere uma maneira de comparar duas frações de denominadores diferentes.

Para comparar duas frações de denominadores diferentes usamos o conceito de frações equivalentes. Se for necessário, recorde o conceito de frações equivalentes seguindo o  link.,

O método é simples. Procuramos duas frações equivalentes às duas frações que desejamos comparar e que, além disto, tenham o mesmo denominador. Clicando neste link você vai conhecer o método matemático usado para encontrar essas frações.

Isto feito, obtemos duas frações de mesmo denominador que representam as mesmas quantidades das frações originais. Comparar uma com a outra é o mesmo que comparar as duas primeiras frações.

 Voltamos ao primeiro caso. Como já sabemos, comparar duas frações de mesmo denominador é fácil: Elas serão iguais se tiverem o mesmo numerador. A maior delas será aquela de maior numerador.

Imagem: portaldoprofessor.mec.gov.br

Aula - Reduzir duas frações ao mesmo denominador.

Qual entre as frações na imagem ao lado é a maior? Note, não dá para compara-las pois elas não têm o mesmo denominador. Não podemos também soma-las ou calcular a diferença entre elas.

Para comparar, para somar ou subtrair duas ou mais frações é necessário primeiro reduzi-las a um denominador comum. Isto significa encontrar duas novas frações, equivalentes às duas primeiras e que tenham o mesmo denominador. Veja o que são frações equivalentes aqui.

A seguir, vamos usar duas pizzas para mostrar, de maneira concreta, a operação matemática de reduzir ao mesmo denominador duas frações.

Temos abaixo duas pizzas de mesmo tamanho, divididas em pedaços iguais. Os pedaços ainda não comidos estão em vermelho e azul e são representados pelas frações mostradas logo abaixo da figura.

Estas duas frações têm denominadores diferentes. O primeiro passo para reduzi-las a um denominador comum é encontrar duas frações equivalentes às primeiras, isto é, frações que representem a mesma quantidade de pizza e que tenham, evidentemente, o mesmo denominador.

Vamos dividir as duas pizzas acima em seis pedaços iguais (linhas tracejadas):

Assim, as frações acima, embora diferentes das primeiras representam as mesmas quantidades de pizza e são, portanto, equivalentes às duas frações originais.

Com isto, temos duas frações diferentes das duas primeiras mas que representam a mesma quantidade de pizza. Isto é, elas representam os mesmos números. Como agora elas têm o mesmo denominador podemos compara-las e operar com elas.

Em termos matemáticos o que fizemos foi o seguinte:

1. Calculamos o mínimo múltiplo comum (M.M.C) entre os denominadores das frações originais, isto é, os números  3 e 2. O M.M.C  entre 2 e 3 é 6. O número 6 é, portanto, o denominador comum que procuramos.
2. Para calcular o numerador das duas novas frações fazemos o seguinte: Para cada uma delas dividimos o MMC ( o número 6, no exemplo ) pelo denominador da fração original e o resultado multiplicamos pelo numerador da fração original. O resultado é o numerador procurado.

Assim:

Com isto reduzimos as duas frações ao mesmo denominador.

Exemplo - Do alto do Himalaia até o fundo do mar.

 O site "Our amazing planet" preparou um interessante cartaz onde mostra, em escala, as medidas de comprimento do relevo da superfície terrestre, desde a altitude de cruzeiro dos jatos, a 11 km de altura, até a parte mais profunda dos oceanos, a fossa das Marianas, no Oceano Pacífico, a 11 km de profundidade. Veja a imagem abaixo.

Antes, porém, preste atenção nessas informações do cartaz:

• A atividade humana vai do topo da troposfera  com os aviões de carreira até a parte mais profunda  fdos oceanos a fossa das Marianas, a 11 km de profundidade;
• Partindo de uma pressão de 1 atm ( uma atmosfera) ao nível do mar, temos uma pressão de  0,3 atm na altura de tráfego dos aviões. A pressão da água, no entanto, varia muito mais. Chega a 1.100 atm na profundidade das fossas das Marianas;
• Acima de 8 km o ar não tem oxigênio suficiente para sustentar a vida humana. A luz solar penetra nas águas do mar até 900 metros de profundidade, embora tubarões, baleias, lulas gigantes e outros animais consigam sobreviver em profundidades maiores;
• Repare nas escalas de temperatura e de pressão. Note ainda a profundidade onde foram encontrados os restos do naufrágio do  navio Titanic.
• Note ainda, do lado direito, a plataforma de petróleo, na superfície, e a linha vermelha que mostra a profundidade de um poço de petróleo no golfo do México. Lembre-se: as profundidades que deverão ser atingidas para alcançar o petróleo no nosso Pré-sal serão bem maiores.

Fonte da imagem: OurAmazingPlanet.com, Exploring the wonder and beauty of planet Earth through exclusive news, features and images.

Exercício - Simplificando frações.

Grande parte das dificuldades apresentadas pelos alunos do ensino médio no aprendizado de ciências e matemática não diz respeito aos conteúdos do nível médio mas às deficiências que eles trazem do ensino fundamental.

Entre  essas deficiências está a de  não saber trabalhar com frações. Se você tem esta dificuldade não adianta ficar se lamentando. Vamos trabalhar para elimina-la.

Para simplificar frações   nada melhor do que começar por identifica-las visualmente. Para isto vamos usar os exercícios do site "Visual fractions". Neste processo iremos usar o conceito de frações equivalentes. Se você desejar recordar a definição de frações equivalentes  clique aqui.

Neste exercício vamos treinar a simplificação de frações, isto é,  vamos encontrar a fração equivalente mais simples que representa a mesma quantidade representada pela fração a ser simplificada.

Para simplificar uma fração devemos dividir ( divisão inteira) o numerador e o denomidador da fração por um mesmo número. Veja a figura abaixo:

Podemos fazer estas divisões por partes. Primeiro tentamos dividir (divisão inteira) o numerador e o denominador da fração por 2. Repetimos o processo até não ser mais possível. Depois tentamos dividr  por 3 e assim sucessivamente, percorrendo a sequência dos números primos (2, 3, 5, 7, ...). A fração estará simplificada quando o numerador e o denominador se tornarem "primos entre si".

No entanto, o melhor e o mais rápido método para  simplificar uma fração é calcular o "Máximo divisor comum" entre o numerador e o denominador da fração a ser simplificada. Depois de calcula-lo dividimos o numerador da fração por ele e obtemos o numerador da fração equivalente mais simples. Fazendo o mesmo com o denominador da fração obtemos o denominador da fração equivalente mais simples.

Vamos então ao exercício. Para isto clique neste link.

Ao abrir a página você notará uma pizza parcialmente comida e os pedaços que restaram em vermelho.  É esta quantidade que está descrita pela fração logo abaixo. Simplifique a fração.

Para conferir a resposta clique no botão "OK". O programa  dará a resposta correta. Note que a pizza correspondente à fração simplificada aparece em azul. Para um novo exercício clique no botão "New example".

Clique na imagem e visite o site Visual Fractions, um guia visual para o aprendizado sobre frações.

Aula - Frações equivalentes.

Grande parte das dificuldades apresentadas pelos  alunos do ensino médio no aprendizado de ciências e matemática não diz respeito aos conteúdos do nível médio mas às deficiências que eles trazem do ensino fundamental. Entre  essas deficiências está a de  não saber trabalhar com frações.

Se você tem essa dificuldade não adianta ficar se lamentando. Vamos trabalhar para elimina-la.

Fração é uma maneira de descrever numericamente uma certa quantidade menor que uma unidade. Você pode recordar a definição de fração seguindo este link. Nesta aula vamos trabalhar com frações equivalentes.

Existem um número infinito de frações para descrever uma mesma quantidade. Estas frações são chamadas de "Frações equivalentes". Repare nas pizzas abaixo. Elas são do mesmo tamanho. Uma delas foi dividida em oito pedaços iguais e a outra em quatro pedaços também iguais.

Da pizza vermelha restam seis oitavos, isto é, seis pedaços ainda não foram comidos. Da pizza azul restam três quartos, ou seja, três pedaços ainda não foram comidos. Note que a quantidade de pizza vermelha que sobrou é a mesma quantidade da pizza azul que ainda resta. No entanto, usamos duas frações diferentes para descreve-las. Estas frações são equivalentes pois descrevem a mesma quantidade de pizza.

Observe ainda que, partindo da pizza azul, podemos construir um número infinito de frações equivalentes para descrever esta mesma quantidade de pizza.  Para isto basta multiplicar o numerador e o denominador da fração 3/4  por um mesmo número inteiro.

Temos então a mesma quantidade de pizza descrita por um número infinito de frações, todas diferentes uma das outras. No entanto, elas serão frações equivalentes às duas primeiras.  

Site interessante - Missão Apollo XI, a chegada do homem na Lua.

No ano de 1969, os astronautas americanos Neil Armstrong e Buzz Aldrin tornaram-se os dois primeiros homens a caminhar no solo lunar. No momento em que toca pela primeira vez o solo da Lua Armstrong pronuncia a frase imortal: " Um pequeno passo para um homem, um grande passo para a humanidade".Também pela primeira vez todo o povo da Terra, através da televisão, está unido, ligado num mesmo acontecimento.

Em comemoração ao 40th aniversário da missão Apollo XI, o John F. Kennedy Presidential Library and Museum   lança o site "We choose de moon". O nome do site é uma referência ao discurso do presidente Kennedy quando do lançamento do programa espacial americano para a Lua.

O site, feito em colaboração com a empresa AOL, recria a viagem da Apollo XI e você pode participar dela acessando o link.  Assista em tela cheia clicando no último botão na parte superior da tela, à direita. O audio da comunicação entre os astronautas e o comando da missão em Houston  é a gravação original da missão.

No site você acompanha o voo da nave Apollo em 11 estágios. Para passar ao próximo estágio clique no botão lateral. Entre cada estágio há um tempo de carregamento do programa. O contador vai até 100. Tenha um pouco de paciência. Vale a pena. Os principais comandos estão mostrados na figura abaixo:

Os estágios da missão são os seguintes:

1. Pré-lançamento. Contagem regressiva em Cabo Canaveral, Florida.
2. Lançamento. A missão começa. Mostra a separação dos vários estágios do foguete Saturno.
3. Órbita. A nave entra em órbita da Terra.
4. Em posição. A nave deixa a órbita de Terra a caminho da Lua.
5. Separação do módulo de comando e acoplamento do módulo Lunar.
6. Ignição do módulo de serviço. Estamos no meio do caminho e a nave acelera rumo à Lua.
7. A nave entra em órbita da Lua. 
8. O módulo Lunar se separa do módulo de serviço.
9. O módulo Lunar inicia a descida rumo à superfície da  Lua.
10. O astronauta Neil Armstrong assume o comando do módulo e o coloca em posição para o pouso.
11. Pouso na Lua. A águia pousou.
    

Com a  animação  aberta e observando a tela você notará que pode avançar para o próximo estágio, ou retornar ao anterior, clicando nos botões laterais " Go to stage..." da parte inferior da tela.

Clicando nos botões azuis pulsantes que aparecem entre os vários estágios da viagem  você tem acesso a vídeos e fotos sobre aquele estágio da missão.

Informação via: http://mashable.com/

Exercício - Construa frações impróprias.

Grande parte das dificuldades apresentadas pelos alunos do ensino médio no aprendizado de ciências e matemática não diz respeito aos conteúdos do nível médio mas às deficiências que trazem do ensino fundamental.

Entre  essas deficiências está a de  não saber trabalhar com frações. Se você tem essa dificuldade não adianta ficar se lamentando. Vamos trabalhar para elimina-la.

Para entender as frações impróprias nada melhor do que começar por identifica-las visualmente. Para isto vamos usar os exercícios do site "Visual fractions". Se você desejar recordar a definição de fração imprópria clique aqui.

Neste exercício você irá representar na forma de fração imprópria um número fracionário escrito na forma mista. Por favor, acesse  os exercícios clicando  aqui.

Para começar clique no botão "start". Você verá algumas pizzas inteiras e outras parcialmente comidas. Abaixo delas estará escrito a forma mista que representa este número. Sua tarefa será escrever na forma de uma fração imprópria o número escrito na forma mista.  Digite a sua resposta como indicado  na figura abaixo e depois clique no botão "OK" para confirmar a resposta.

Se você acertar aparecerá a expressão "correct" abaixo do desenho das pizzas juntamente com a fração imprópria correta. O botão "New example" acenderá em vermelho. Clique nele para prosseguir.

Se errar...bom, tente novamente digitando a sua resposta e, em seguida clique no botão "OK" para confirmar.

A quantidade de acertos e de tentativas erradas, assim como o percentual de acertos será computada no painel à esquerda, na parte superior.

Clique na imagem e visite o site Visual Fractions, um guia visual para o aprendizado sobre frações.

Aula - Frações impróprias.

Grande parte das dificuldades apresentadas pelos  alunos do ensino médio no aprendizado de ciências e matemática não diz respeito aos conteúdos do nível médio mas às deficiências que eles trazem do ensino fundamental. Entre  essas deficiências está a de  não saber trabalhar com frações.

Se você tem essa dificuldade não adianta ficar se lamentando. Vamos trabalhar para elimina-la.

Fração é uma maneira de descrever numericamente uma certa quantidade menor que uma unidade. Reveja a definição de fração consultando este link.

Considere que você esteja numa situação de poder dispor de três pizzas inteiras e uma outra parcialmente comida. Pizzas como estas da figura abaixo.

Uma opção é usar uma forma mista, isto é, usar números inteiros e frações. As duas pizzas inteiras são, claro, descritas pelo número 2 enquanto a pizza parcialmente comida é descrita por uma fração. Teríamos então:

Em palavras: Possuo duas pizzas inteiras e cinco doze avos de uma terceira.

Outra opção para descrever esta quantidade é usar somente as frações. No entanto, frações são, por definição, números menores que a unidade e este não é o caso aqui. Por isto a fração que vamos usar é chamada de fração imprópria. Ela é construida a partir da forma mista multiplicando-se o denominador da fração pelo número inteiro. Depois somamos o resultado ao numerador da fração. Este resultado será o numerador da fração imprópria:

O denominador da fração imprópria será o denominador da parte fracionária da forma mista:

A característica da fração imprópria é possuir o numerador maior que o denominador. Para retornar à forma mista basta fazer a divisão inteira de 29 por 12.