Aula - A trajetória parabólica do lançamento horizontal.

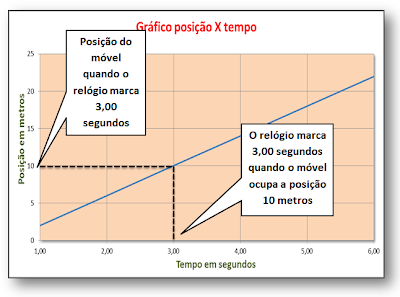
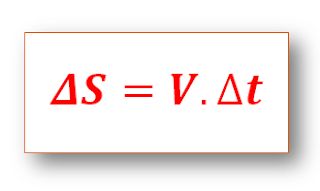Um objeto, próximo à superfície terrestre, lançado com uma velocidade de direção horizontal, segue uma trajetória parabólica. Claro, estamos fazendo algumas simplificações. Estamos assumindo que a única força  agindo sobre o objeto é a força gravitacional.

Galileu percebeu que este movimento de trajetória parabólica poderia ser entendido como a soma vetorial de dois outros movimentos que ele conhecia bem: O movimento retilíneo uniforme, na horizontal, e o movimento retilíneo uniformemente acelerado, na vertical.

Abra a animação. Clique sobre a imagem para inicia-la. A bola vermelha é lançada horizontalmente a partir da plataforma no ponto "a". As retas que formam a grade do desenho são marcadas em tempos iguais. A bola vermelha segue a trajetória "ifh". Esta trajetória é parabólica.

O que Galileu propôs foi o seguinte: Imagine que a bola vermelha tenha dois fantasmas ( as bolas de cor rosa ) que seguem o seu movimento. Uma o faz pela horizontal e a outra pela direção vertical.

O fantasma da horizontal segue uma trajetória retilínea com velocidade constante. Observe que as distâncias entre as retas e, d, c e b são constantes. O movimento é então retilíneo uniforme.

Na vertical atua a força gravitacional. Isto implica que o movimento é uniformemente acelerado. Observe as distâncias entre as retas b, g, l e n, elas são progresivamente maiores.

Abra a animação. Desenhe numa folha de papel as setas do vetor velocidade na horizontal e do vetor velocidade na vertical em vários pontos ao longo da trajetória. Some as setas duas a duas. Você verificará que o vetor soma é sempre tangente à trajetória parabólica.

Lembre-se: A seta horizontal é sempre do mesmo tamanho pois o movimento é uniforme. A seta vertical, por sua vez, é progresivamente maior pois o movimento na vertical é acelerado.

Sugestão: Para desenhar as setas escolha os pontos b, i, f e h. Note que no ponto b a velocidade vertical da bola vermelha é nula pois a aceleração da gravidade ainda não teve tempo de agir.

Animação produzida por: Michael Fowler, professor do departamento de Física da Universidade da Virgínia.

Imagem: kleberandrade.wordpress.com

Aula - Gráfico posição x tempo do movimento uniformemente variado - velocidade.

Abaixo temos a função quadrática ou função do segundo grau de variável "x". Sabemos que o seu gráfico é uma parábola.

Note a semelhança entre as equações. Podemos enxergar a equação horária do movimento uniformemente acelerado ( MRUV ) como uma função do segundo grau de variável "t".

Assim, o termo independente "c" passa a ser a posição inicial; o termo "b" a velocidade inicial e "a" a metade da aceleração do objeto.

Vamos usar a animação abaixo para verificar quais informações podemos obter  do gráfico posição x tempo do MRUV no que se refere a velocidade do objeto. Como o movimento é acelerado a velocidade, claro, muda a cada instante. Vamos usar a inclinação da reta tangente para comparar as seus valores.

A reta tangente no ponto A está inclinada para a esquerda, o que informa que a velocidade é negativa naquele ponto. O objeto está se aproximando da origem. No ponto C a reta tangente está inclinada para a direita. Isto informa que a velocidade é positiva no ponto C. O objeto está se afastando da origem. Repare ainda que a reta tangente está, em relação ao eixo horizontal, mais inclinada em A que em C. Isto informa que o módulo da velocidade é maior em A.

Observe a reta tangente no ponto B. Ela é paralela ao eixo horizontal. Sua inclinação é nula. Isto nos informa que a velocidade nesse ponto é nula. No ponto B o objeto inverte o sentido do seu movimento.

Na animação abaixo, mova os controles e marque o valor negativo para "a". Reproduza a parábola numa folha de papel. Marque  retas tangentes em vários pontos e compare o valor da velocidade nesses pontos.

Animação produzida por The PhET Interactive Simulations Project da  Universidede do Colorado, Boulder.

Aula - Gráfico posição x tempo do Movimento uniformemente variado - aceleração.

Abaixo temos a função quadrática ou função do segundo grau de variável "x". Sabemos que o seu gráfico é uma parábola.

Podemos enxergar a equação horária do movimento uniformemente acelerado ( MRUV ) como uma função do segundo grau de variável "t".

Assim, o termo independente "c" passa a ser a posição inicial; o termo "b" a velocidade inicial e "a" a metade da aceleração do objeto.

Vamos usar a animação abaixo para verificar quais informações podemos obter  do gráfico posição x tempo do MRUV no que se refere a aceleração.

Clique no botão vermelho "zero" para iniciar a animação.

1. Deixe o termo "ax²" nulo, isto é, a aceleração nula. Arraste o botão referente ao termo "bx". Dê a ele valores positivos e negativos. Veja que o gráfico do movimento é uma reta, isto é, como a aceleração é nula o movimento é uniforme.
2. Clique novamente no botão "zero". Agora movimente o botão referente ao termo "ax²". Dê a ele valores positivos. Observe que a concavidade da curva é para cima e que quando maior o valor mais estreita é a parábola. Assim, quando observar o gráfico posição x tempo, se a concavidade da curva é para cima saberá que a aceleração do movimento é positiva, isto é, tem o sentido positivo do eixo. E mais: quanto mais estreita a parábola maior é o módulo da aceleração.
3. Clique novamente no botão "zero". Continue movimentando o botão referente ao termo "ax²". Agora, dê a ele valores negativos. Observe que a concavidade da curva é para baixo e que quando maior (em módulo) o valor mais estreita é a parábola. Assim, quando observar o gráfico posição x tempo, se a concavidade da curva é para baixo saberá que a aceleração do movimento é negativa, isto é, tem o sentido negativo do eixo. E mais: quanto mais estreita a parábola maior é o módulo da aceleração.
   

Animação produzida por The PhET Interactive Simulations Project da  Universidade do Colorado, Boulder.

Exemplo - Campo magnético.

Os campos magnéticos mais notáveis ao nosso alcance estão no sol e nos planetas. Eles, claro, não podem ser vistos diretamente, mas podemos ter uma ideia precisa da direção das suas linhas de campo quando eles interagem com a matéria expelida pelo sol e que forma o  vento solar.

As partículas que compõem o vento solar são carregadas eletricamente e estão em movimento. Portanto sofrem uma aceleração na presença de um campo magnético. Isto acontece quando elas atingem a atmosfera dos planetas. Por exemplo,ao atingir a Terra elas se movem ao longo das linhas do campo magnético do planeta e se concentram nos polos magnéticos. Lá elas interagem com as moléculas do ar presentes na alta atmosfera que, por sua vez, emitem luz formando as auroras boreais e austrais.

As fotos abaixo foram tiradas em órbita da Terra e captam uma amostra dessa luz.A forma da matéria luminosa dá uma ideia das linhas do campo magnético. Observe as fotos.

O mesmo ocorre nos outros planetas. No vídeo abaixo temos imagens da Aurora boreal no planeta Júpiter. Foram captadas na faixa de frequência da luz ultravioleta pelas câmaras do Telescópio Espacial Hubble, em 2007.

No vídeo abaixo temos uma aurora no polo sul de Saturno captadas do mesmo modo e na mesma data. Repare, na lateral direita dos vídeos, a escala de intensidade. Nela o branco representa a faixa mais intensa da radiação.

Imagens e vídeos: NASA, Boston university.

Aula - Adição de dois vetores perpendiculares entre si.

O método gráfico de adição de vetores (modelo das setas) que estamos usando é completo. Fornece módulo, direção e sentido do vetor soma, mas para isto devemos usar uma escala conveniente. No ensino médio não damos muita importância para a escala. Geralmente nos contentamos em obter a direção, o sentido e o módulo aproximado do vetor resultante.

Em certas situações especiais podemos obter o valor do módulo com exatidão. Uma dessas situações surge quando somamos dois vetores com direções perpendiculares entre si. Neste caso os vetores e a resultante  formam um triângulo retângulo e isto nos permite calcular o módulo pelo teorema de Pitágoras.

Na animação abaixo usamos o método do paralelogramo para somar dois vetores perpendiculares entre si. Esta situação é muito comum na Física. Ela aparece quando queremos calcular as componentes perpendiculares de um vetor.Por isto você deve estudar a animação com bastantes atenção.

Na a animação clique no botão "]<<" para retornar ao início da apresentação e vá clicando no botão ">>" para avançar a apresentação passo a passo.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Aula - A inclinação da reta e a taxa de variação entre duas grandezas.

Na equação da reta abaixo o número "m" é chamado coeficiente angular. Ele nos fornece uma medida da inclinação da reta em relação ao eixo horizontal do gráfico. O número "b", por sua vez, é chamado coeficiente linear e fornece o ponto onde a curva cruza o eixo vertical.

Isto para a matemática. Na Física, no entanto, o gráfico cartesiano é uma fotografia do relacionamento entre duas grandezas cujas medidas estão marcadas nos eixos.

Neste caso,  o coeficiente angular nos dá a medida da taxa de variação da grandeza representada no eixo vertical em relação à grandeza representada no eixo horizontal.

Assim, se no eixo vertical temos representada a posição e no eixo horizontal o tempo e o gráfico cartesiano é uma reta então temos o movimento uniforme:

Neste caso, o coeficiente angular nos dá a medida de quanto a posição ( S ) varia por cada unidade de tempo, isto é, a velocidade ( V ). O coeficiente linear dá a posição inicial do objeto.

Do mesmo modo, se no eixo vertical temos representada a velocidade de um objeto ( V ) e no eixo horizontal o tempo ( t ) e o gráfico cartesiano é uma reta então temos o movimento uniformemente variado:

Neste caso, o coeficiente angular nos dá a medida de quanto a velocidade do objeto varia por cada unidade de tempo, isto é, a aceleração ( a ). O coeficiente linear nos dá a velocidade inicial do objeto.

Em todos esses casos temos uma grandeza que varia proporcionalmente  a outra grandeza. Essa situação é bastante comum na natureza. Somente para dar mais um exemplo citamos a quantidade de calor ( Q ) transferida entre dois sistema:

Aqui, no eixo vertical temos a quantidade de calor transferida e no eixo horizontal a temperatura .Nesse caso, o coeficiente angular nos dá a medida  a quantidade de calor transferida por cada unidade de variação da temperatura ( delta T ), isto é, a capacidade térmica do sistema ( C ).

Use a animação abaixo e faça os exercícios. Marque as coordenadas dos pontos nas caixas Point1 e Point2, clique no botão "Solve" e leia "m" e "b".

1. Calcule a capacidade térmica de um sistema cujo gráfico QxT passa pelos pontos (0,0) e (4,7)
2. Calcule a posição inicial e a velocidade de um objeto cujo gráfico Sxt passa pelos pontos ( 3,3) e (5,5).
3. Calcule a aceleração e a velocidade incial de um objeto cujo gráfico Vxt passa pelos pontos (4,5) e (8,7).

Poodwaddle.com

Exercício - Inclinação positiva e negativa de uma reta.

Na equação da reta abaixo o número "m" é chamado coeficiente angular. Ele nos fornece uma medida da inclinação da reta em relação ao eixo horizontal do gráfico.

Vamos usar a animação a seguir para fazer alguns exercícios para que você adquira uma visão clara de como se comporta a reta em função do valor de "m".

Na caixa "b" digite zero. Na caixa "m" digite sucessivamente 0.1; 0.5; 0.8; 1; 5; 10 e 20. Clique no botão "Solve", após digitar cada número, para desenhar a reta.

Atenção:  A animação usa a notação inglesa. Portanto escrevemos 0.5 ( zero ponto cinco ) em vez de 0,5 ( zero vírgula cinco )

Note: Se "m" é positivo a inclinação é para a direita.  À medida que o valor de "m" cresce positivamente a reta aumenta a sua inclinação em relação à horizontal e se aproxima do eixo vertical.

Na caixa "b" digite zero. Na caixa "m" digite sucessivamente -0.1; -0.5; -0.8; -1; -5; -10 e -20. Clique no botão "Solve", após digitar cada número, para desenhar a reta.

Note:  Se "m" é negativo a inclinação da reta é para a esquerda. À medida que o valor de "m" cresce em módulo a reta aumenta a sua inclinação e se aproxima do eixo vertical.

Animação produzida por: Poodwaddle.com

Aula - Velocidade média no movimento uniformemente acelerado.

Para qualquer tipo de movimento a velocidade média é definida como a razão entre a variação da posição e o intervalo de tempo correspondente, isto é, o intervalo de tempo em que a variação  da posição ocorre.

Para o movimento com aceleração constante temos uma segunda opção para o cálculo da velocidade média. Este movimento é retilíneo e sua velocidade varia uniformemente com o tempo. Neste caso, e somente neste caso, a velocidade média é a média das velocidades do início e do final do intervalo de tempo.

Em termos matemáticos:

Onde V1 é a medida da velocidade instantânea no início do intervalo de tempo comsiderado e V2 a medida dela no final do intervalo de tempo.

Use as equações abaixo e calcule a velocidade média desse movimento entre os instantes t1 = 2,0 s e t2 = 4,0 s. As unidades das grandezas são as do SI.

Resposta: 34 m/s.

Aula - Subtração de vetores. Modelo gráfico.

A subtração do vetor a pelo vetor b pode ser definida como a soma do vetor a com vetor oposto do vetor b.

Em termos matemáticos temos:

Em termos geométricos o vetor oposto é um vetor com o mesmo módulo e direção do vetor original e com sentido inverso, isto é, a seta que representa o vetor sofreu um giro de 180 graus.

Vamos usar a animação abaixo para subtrair o vetor b do vetor a. Clique no botão " ]<< " para retornar ao inicio. Clique no botão " >> "  para avançar a animação passo a passo.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Exercício - Método da área sob a curva, velocidade variável.

Para um gráfico cartesiano do tipo Velocidade X tempo a área sob a curva do gráfico, isto é, a área entre a curva e o eixo horizontal,  mede a distância percorrida pelo objeto cujo movimento o gráfico descreve.

Na animação abaixo temos o gráfico velocidade X tempo de um objeto em movimento. Desta vez, porém, o movimento é acelerado. Neste caso a aceleração é constante e, portanto, a velocidade cresce linearmente com o tempo. O gráfico da velocidade é uma reta.

Clique no ponto azul e arraste. Você marcará o instante de tempo inicial desejado. Faça o mesmo para o botão vermelho e marcará o instante de tempo final. A área sob a curva é marcada em rosa e a sua medida, que fisicamente significa a distância percorrida no intervalo de tempo que você escolheu, será dada em " e = ..."

Note que  a velocidade é positiva do início do movimento até o relógio marcar 5,0 segundos. Neste intervalo de tempo a velocidade vai diminuindo de valor. O objeto está se movimentando no sentido positivo da sua trajetória. Quando o relógio marca 5,0 segundos a velocidade se anula e o sentido do movimento se inverte. Daí para frente a velocidade é negativa e cresce em módulo. O objeto está agora se movimentando no sentido negativo da sua trajetória.

Quando calculamos a área sob a curva teremos uma área positiva até 5,0 s e negativa a partir daí. A área total, isto é, a distância percorrida pelo objeto, é dada pela soma algébrica ( levando em conta o sinal ) das duas áreas parciais.
  

Vamos fazer alguns exercícios. A resposta será dada em e = ...

• Marque o instante inicial do movimento em 3,0s e o final em 5,0 s
• Marque o instante inicial do movimento em 5,0 s e o instante final em 7,0 s.
  
• Marque o instante inicial do movimento em 3,0 s e o instante final em 7,0 s. Note que ás áreas marcadas encima e embaixo da curva são iguais. A área é positiva entre 3,0 e 5,0 s e negativa entre 5,0 e 7,0 s. Isto significa que o objeto se movimentou no sentido positivo da trajetória até  o relógio marcar 5,0s, deu meia volta e retornou ao ponto de partida. No final das contas ele não saiu do lugar. A distância. claro, é nula.
• Calcule a distância percorrida entre o inicio do movimento (t=0)e t= 9,0s.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Exercício - Método da área sob a curva, área negativa.

Para um gráfico cartesiano do tipo Velocidade X tempo a área sob a curva do gráfico, isto é, a área entre a curva e o eixo horizontal,  mede a distância percorrida pelo objeto cujo movimento o gráfico descreve.

Na animação abaixo temos o gráfico velocidade X tempo de um objeto com velocidade constante. Clique no ponto azul e arraste. Você marcará o instante de tempo inicial desejado. Faça o mesmo para o botão vermelho e marcará o instante de tempo final. A área sob a curva é marcada em rosa e a sua medida, que fisicamente significa a distância percorrida no intervalo de tempo que você escolheu, será dada em " d = ..."

Note que neste caso a velocidade é negativa. Isto significa que o objeto está se movimentando no sentido negativo do eixo. Quando calculamos a área sob a curva teremos uma área negativa. Claro, não existe uma área negativa em termos geométricos. Lembre-se, no entanto, que estamos dando um significado físico para a área: Para nós ela significa a distância que o objeto percorreu.

 Neste caso, a área negativa  significa apenas que o objeto  percorreu esta distância no sentido negativo do eixo.
  

Vamos fazer alguns exercícios:

•  Calcule a distância percorrida entre o início do movimento e o instante 6,0 segundos.
• Calcule a distância percorrida entre os instantes 2,2 s e 10 s.
• Calcule a distância percorrida  entre os instantes 4,5 s e 7,5 s.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Exercício - Método da área sob a curva.

Para um gráfico cartesiano do tipo Velocidade X tempo a área sob a curva do gráfico mede a distância percorrida pelo objeto cujo movimento o gráfico descreve.

Na animação abaixo temos o gráfico velocidade X tempo de um objeto com velocidade constante. Clique no ponto azul e arraste. Você marcará o instante de tempo inicial desejado. Faça o mesmo para o botão vermelho e marcará o instante de tempo final. A área sob a curva é marcada em rosa e a sua medida, que fisicamente significa a distância percorrida no intervalo de tempo que você escolheu, será dada em " d = ..."

Vamos fazer alguns exercícios:

•  Calcule a distância percorrida entre o início do movimento e o instante 4,0 segundos.
• Calcule a distância percorrida entre os instantes 2,0 s e 10 s.
• Calcule a distância percorrida  entre os instantes 5,5 s e 9,5 s.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Exemplo - Auto indução no circuito elétrico.

Um condutor percorrido por uma corrente elétrica produz em torno de si um campo magnético. Quando este campo varia ele induz ou cria no condutor uma corrente elétrica adicional sempre num sentido tal que tende a impedir a variação da corrente original.

Circuitos que possuem muitos  aparelhos elétricos com bobinas entre seus componentes têm  coeficiente de auto indução alto. Nestes casos a corrente auto induzida pode atingir níveis elevados.

Assim, quando desligamos um circuito com pequeno coeficiente de auto indução a corrente cai rapidamente a zero ( Veja figura abaixo, na linha tracejada ). De modo contrário, quando o circuito possui  coeficiente   de auto indução grande a corrente auto induzida produz um crescimento momentâneo da corrente elétrica  ( Veja a figura, na linha contínua ) provocando aquelas faíscas que você certamente já observou. 

Uma maneira de evitar este fenômeno é diminuir o tempo de desligamento do circuito. Isto é conseguido com o uso de disjuntores. Veja no vídeo abaixo a que níveis de intensidade a faísca pode chegar.

Aula - Os gráficos na Física. Leitura indireta 2.

A função de um gráfico é fornecer informações. Algumas são obtidas pela leitura direta nas escalas dos eixos do gráfico. Outras são obtidas de maneira indireta, isto é, são necessários alguns cálculos prévios. Um desses métodos de tirar informações dos gráficos é o Método da área sob a curva. Para o gráfico VelocidadeX tempo ele calcula a distância percorrida entre dois instantes no tempo.

Da definição de velocidade média obtemos a seguinte relação:

Este método vale para qualquer tipo de movimento. Agora, no entanto, vamos trabalhar com o movimento retilíneo uniforme. Neste caso, o gráfico da velocidade é uma reta paralela ao eixo horizontal uma vez que a velocidade é constante.

Observe o gráfico abaixo. No eixo vertical temos marcada  a velocidade, no eixo horizontal o tempo. O produto da velocidade pelo intervalo de tempo corresponde, em termos geométricos, à área do retângulo rosa. Fisicamente esta área fornece a distância percorrida pelo objeto neste intervalo de tempo.

Aula - Os gráficos na Física. Leitura indireta 1.

A função de um gráfico é fornecer informações. Algumas são obtidas pela leitura direta nas escalas dos eixos do gráfico. Outras são obtidas de maneira indireta, isto é, são necessários alguns cálculos prévios. Um desses métodos de tirar informações dos gráficos é o Método da Taxa de variação entre duas grandezas. Para o gráfico Posição X tempo ele calcula a velocidade. O método serve para qualquer tipo de movimento.

Da Geometria analítica sabemos que o gráfico de uma função linear, ou função de primeiro grau, é uma reta. Observe a função f(x) abaixo. Ela é uma função linear. O número "a" é chamado coeficiente angular da reta. Ele dá a inclinação da reta em relação ao eixo horizontal. Quanto maior for "a", mais inclinada a reta estará.

O coeficiente angular da reta é calculado por:

Se "a" for um número positivo a reta estará inclinada para a direita. Se for um número negativo a reta estará inclinada para a esquerda.

A expressão matemática para o movimento retilíneo uniforme acima  é uma função linear logo o seu gráfico é uma reta. Note que a velocidade "v" está no lugar de "a". Assim a inclinação da reta fornece a velocidade do movimento. 

Umas das características de uma reta é ter a inclinação constante. Logo, escolhendo um "delta t" qualquer e tomando o "delta S" correspondente no gráfico do movimento retilíneo uniforme podemos calcular a velocidade do movimento.

Aula - O espectro eletromagnético.

Quando aceleramos uma partícula que possui carga elétrica ela emite energia para o espaço a sua volta. Este tipo de fenômeno tem muitas semelhanças com uma onda na superfície da água.

Estas ondas são causadas pela variação do campo elétrico e do campo magnético da partícula e são, portanto, chamadas de ondas eletromagnéticas. Elas têm duas características notáveis:

• Uma onda na superfície da água necessita dela para se propagar. Se não há água não existe onda. As ondas eletromagnéticas, no entanto,  têm a propriedade de se propagar no vácuo.
• As ondas eletromagnéticas são o que existe de mais veloz na natureza. No vácuo, elas se propagam na velocidade da luz.

Imagine uma partícula com carga elétrica num movimento de "vai-e-vem". Esse movimento tem uma frequência que, por sua vez, é a frequência da onda que a partícula emite. Ao conjunto de ondas de todas as frequências possíveis chamamos de "espectro eletromagnético".

Um pequeno intervalo dessas frequências são capazes de sensibilizar as células da retina dos nosso olhos. Nosso cérebro processa essas informações e nos as percebemos  como as cores mostradas abaixo. Essa parte do espectro eletromagnético é chamado "espectro visível da luz".

Nós usamos as ondas eletromagnéticas para transportar informação e essa aplicação tecnológica determinou a divisão do espectro em várias regiões: ondas de rádio, micro-ondas, televisão,etc.

Abra a animação. Ela foi preparada pelo CPTEC ( Centro de Previsão de Tempo e Estudos Climáticos ) do INPE ( Instituto Nacional de Pesquisas Espaciais ) e mostra as faixas de frequências em que está dividido o espectro eletromagnético bem como as características de cada uma delas.

Aula - Os gráficos na Física. Leitura direta.

Os gráficos são a maneira mais eficiente que temos de exibir informações. Permitem uma análise rápida dos dados.

Portanto, gráfico não é um enfeite. Se ele aparece num determinado problema tenha certeza: Ele está ali para você retirar dele as informações necessárias para a resolução da questão.

Algumas dessas informações são obtidas por leitura direta. Para isto é necessário ler o rótulo de cada um dos eixos. Repare na grandeza exibida e na unidade. Veja o gráfico abaixo.

Se for necessário saber qual a posição do móvel quando o relógio marca 3,00 segundos levante uma paralela ao eixo vertical passando pelo ponto 3,00 do eixo horizontal até encontrar a curva ( linha azul ) e dai trace uma paralela ao eixo horizontal até encontrar o eixo vertical. Leia a informação na escala do eixo vertical: 10 m.

Se, por outro lado, for necessário saber qual a marcação do relógio quando o móvel ocupa a posição 10 metros faça o caminho inverso. Levante uma paralela ao eixo horizontal passando pelo ponto 10 m do eixo vertical até encontrar a curva ( linha azul ) e dai trace uma paralela ao eixo vertical até encontrar o eixo horizontal. Leia a informação na escala do eixo horizontal: 3,00 s.

Aula - As fórmulas matemáticas na física.

Na Física, para falar de como duas ou mais grandezas se relacionam usamos a linguagem matemática, isto é, usamos uma fórmula.

Na fórmula cada grandeza é representada por uma letra. Os números que colocados no lugar das letras são o resultado de medidas realizadas previamente por alguém com o instrumento de medida adequado. Portanto eles não são apenas números. São números e suas unidades.

Ao manipularmos uma fórmula temos que nos certificar se as unidades são compatíveis umas com as outras. Para facilitar este trabalho foi criado o Sistema Internacional de Unidades. Nele as unidades são compatíveis uma com as outras.

Por exemplo: Se você calcula o valor de uma força usando a fórmula da segunda lei de Newton e mede o valor da massa em quilograma e o valor da aceleração em m/s² obterá a força em Newton. Se não o fizer obterá o valor correto da força mas  em outra unidade.

Observe ainda: